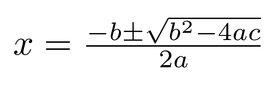Advanced Algebra
POW 1 Poster
This is a revised Problem of the Week I displayed at my school exhibition.
Check Point
3/3/17
Complex Numbers
Complex numbers can be written as a+bi, a-bi, a*bi, or a/bi. ”I” represents an imaginary numbers. When i is squared i2it equals -1, any imaginary number squared can equal a real number. The a and b can be represented by any real number. Real numbers include all rational and irrational numbers. Complex numbers are the combination of real and imaginary numbers.
Examples:
Multiplying Complex Numbers
(1-5i)(3+3i)
Adding Complex Numbers
(7+2i)+(4-10i)
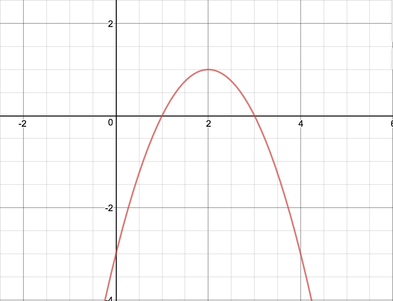
Evaluate and Interpret the Quadratic Equation
f(x)= -x^2+4x-3
Complex numbers can be written as a+bi, a-bi, a*bi, or a/bi. ”I” represents an imaginary numbers. When i is squared i2it equals -1, any imaginary number squared can equal a real number. The a and b can be represented by any real number. Real numbers include all rational and irrational numbers. Complex numbers are the combination of real and imaginary numbers.
Examples:
Multiplying Complex Numbers
(1-5i)(3+3i)
- Distribute 1 to 3 and 3i. You should get 3+3i.
- Now distribute -5ito 3 and 3i. You should get -15i and- 15i2.
- Now have 3+3i-15i-15.
- Simplify to 3-12i-15i2.
- i2is equal to negative one plug -1 in for i2.
- 3-12i-15(-1)can be solved to 18-12i.
Adding Complex Numbers
(7+2i)+(4-10i)
- Find like terms. (7+2i)+(4-10i)
- Now combine the like terms together. 7+4=11 and 2i-10i=-8i
- Your answer is 11- 8i
Evaluate and Interpret the Quadratic Equation
f(x)= -x^2+4x-3
- The first thing you can get from looking at the equation is the y-intercept. Which is -3 in standard form it should always be the last value.
- You can find the x-intercepts by using the quadratic equation ( below). You will get two answers for x because the + and - in the quadratic equation. Your x-intercepts will be (1,0) and (3,0) .
- Now, you can find the vertex, the highest or lowest point of the parabola, you must find the axis of symmetry first. To find the axis of symmetry, the middle of the two x-intercepts, use the equation -b/2a. The parabola above has an axis of symmetry of 2. Now plug to our equation for x, -2^2+4(2)-3=1. The vertex is (2,1).
- Moving on, you can find the focus of the parabola by using the equation 14a, in the parabola this would be 1/ 4(-1). That equals -.25. Subtract that from your the y value in the vertex. You should get (0, .75) as your focus.
Problem of the Week
Amaya Holliday's Long Walk Home POW by Amaya on Scribd